查找和排序是算法中很基础也很关键的两块内容,其中排序算法众多,让人容易混乱,真正使用时又不知如何下手,本文就对各大算法进行比较,并归纳总结他们适用的地方。
直接插入排序
直接插入排序算是插入排序的一种,也可以说是插入排序的狭义代换。直接插入排序的数据情况为(有序区,无序区)。把无序区的第一个元素插入到有序区的合适的位置。对数组来说,比较得少,换得多。如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找插入排序。插入排序不适合对于数据量比较大的排序应用。基本有序或者 n 比较小的时候应选择插入排序,而基本倒序则不适合使用插入排序。大多数排序算法都是使用线性存储结构,像插入排序这种算法用链表实现更好,省去了移动元素的时间。
希尔排序
希尔排序是直接插入排序的改进版,算是插入排序的一种。直接插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率,但每次只能将数据移动一位,所以才有了希尔排序的产生。原始的算法实现在最坏的情况下需要进行 O(n2) 的比较和交换,希尔排序通过将比较的全部元素分为几个区域来提升直接插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
例如,假设有这样一组数 [13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10],如果我们以步长为 5 开始进行排序,我们可以通过将这列表放在有 5 列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
然后我们对每列进行排序:
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
将上述四行数字,依序接在一起时我们得到:[10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45]。这时 10 已经移至正确位置了,然后再以 3 为步长进行排序:
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
排序之后变为:
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
最后以 1 步长进行排序(此时就是简单的插入排序了)。
简单选择排序
简单选择排序算是选择排序的一种,也可以说是选择排序的狭义代换。简单选择排序的数据情况为(有序区,无序区)。在无序区里找一个最小的元素跟在有序区的后面。对数组来说,比较得多,换得少。选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。最好情况是,已经有序,交换 0 次;最坏情况是,逆序,交换 n - 1 次。交换次数比冒泡排序较少,由于交换所需 CPU 时间比比较所需的 CPU 时间多,n 值较小时,选择排序比冒泡排序快。原地操作几乎是选择排序的唯一优点,当空间复杂度要求较高时,可以考虑选择排序;实际适用的场合非常罕见。
堆排序
堆排序也是选择排序的一种,是简单选择排序的改进版,常用来排出前几大的数。当n较大时,可以考虑采用堆排序。
冒泡排序
冒泡排序是交换排序的一种,冒泡排序的数据情况为(无序区,有序区)。从无序区通过交换找出最大元素放到有序区前端。
对于冒泡排序,可以设置一个标记,若某一趟遍历没有数据交换,则说明已排好序,因此可以直接退出排序。具体代码如下:
// 冒泡排序的优化1
#include <stdio.h>
#include <stdlib.h>
int n;
int *s;
int data_input = 1;
int myarray[10] = {1, 0, 4, 2, 7, 1, 5, 6, 8, 7};
void sort(int *arr) {
int i, j, k;
for(i = 0; i < n - 1; i++) {
int flag = 1;
for(j = 0; j < n - i - 1; j++) {
if(arr[j] > arr[j + 1]) {
arr[j] = arr[j] ^ arr[j + 1];
arr[j + 1] = arr[j + 1] ^ arr[j];
arr[j] = arr[j] ^ arr[j + 1];
flag = 0;
}
}
for(k = 0; k < n; k++) {
printf("%d ", arr[k]);
}
printf("\n");
if(flag == 1) {
break;
}
}
printf("\nHere is the result after sorting:\n");
for(k = 0; k < n; k++) {
printf("%d ", arr[k]);
}
printf("\n");
}
int main() {
int i;
if(data_input == 0) {
printf("Please input the number of data:\n");
scanf("%d", &n);
s = (int *)malloc(sizeof(int) * n);
printf("Please input the data:\n");
for(i = 0; i < n; i++) {
scanf("%d", &s[i]);
}
sort(s);
} else {
n = sizeof(myarray) / sizeof(int);
sort(myarray);
}
}
也可以记录某次遍历时最后发生数据交换的位置,这个位置之后的数据显然已经有序,不用再排序了。因此通过记录最后发生数据交换的位置就可以确定下次循环的范围了。代码如下:
// 冒泡排序的优化2
#include <stdio.h>
#include <stdlib.h>
int n;
int *s;
int data_input = 1;
int myarray[10] = {1, 0, 4, 2, 7, 1, 5, 6, 8, 7};
void sort(int *arr) {
int i, j, k, range, n0;
//range为循环的范围,初始值n-1
range = n - 1;
for(i = 0; i < n - 1; i++) {
int flag = 1;
//只遍历到最后交换的位置即可
n0 = range;
for(j = 0; j < n0; j++) {
if(arr[j] > arr[j + 1]) {
arr[j] = arr[j] ^ arr[j + 1];
arr[j + 1] = arr[j + 1] ^ arr[j];
arr[j] = arr[j] ^ arr[j + 1];
//记录最后交换的位置
range = j;
flag = 0;
}
}
for(k = 0; k < n; k++) {
printf("%d ", arr[k]);
}
printf("\n");
if(flag == 1) {
break;
}
}
printf("\nHere is the result after sorting:\n");
for(k = 0; k < n; k++) {
printf("%d ", arr[k]);
}
printf("\n");
}
int main() {
int i;
if(data_input == 0) {
printf("Please input the number of data:\n");
scanf("%d", &n);
s = (int *)malloc(sizeof(int) * n);
printf("Please input the data:\n");
for(i = 0; i < n; i++) {
scanf("%d", &s[i]);
}
sort(s);
} else {
n = sizeof(myarray) / sizeof(int);
sort(myarray);
}
}
快速排序
快速排序是交换排序的一种,属于冒泡排序的改进。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。当待排序的关键字是随机分布时,快速排序的平均时间最短。
归并排序
归并排序由冯诺依曼提出,采用到分治法的思想。
基数排序
基数排序是一种非比较型整数排序方法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
计数排序
计数排序也不是比较排序,排序速度快于任何比较排序,应用于输入元素是n个0到k之间的整数的情况。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。
总结
这里我们只列举了九种排序方法,其中冒泡法、插入法以及选择法是比较基础的排序方法,而快排和堆排序相对则是比较难一点,但同样非常重要。对于桶排序、鸽巢排序等等我们则不作介绍,具体可以查看维基百科的排序算法词条。
对于前面讲的几个算法,我们可以通过下图总结一下:
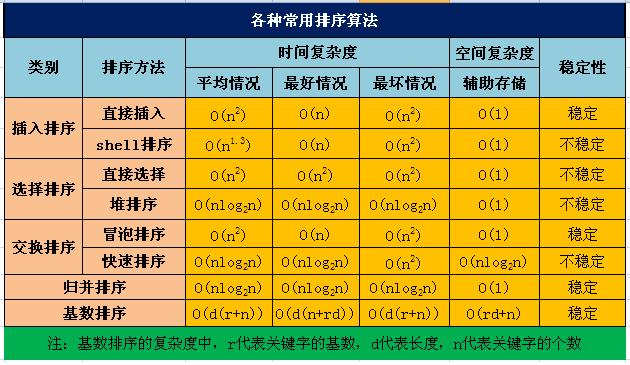
附:关于稳定性
- 稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序
- 不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序